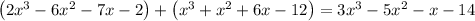Answer:
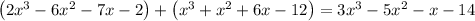
Explanation:
To add the polynomials
Remove parentheses:
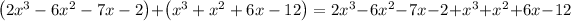
Group like terms:
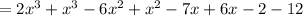
Add similar elements:
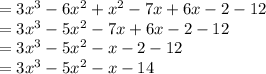
The Standard Form for writing down a polynomial is to put the terms with the highest degree first,its term of 2nd highest is 2nd etc..
In our case the standard form is