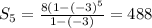Question

Find the sum of the first five terms of the geometric series 8, −24, 72, …

484
488
648
684

Answer 1

The sum of first five terms are
`S_(5) = 8 -24 +72 -216 +648 = 488`

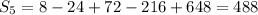
Explanation:

Step 1:-

sequence:- an ordered pair of real numbers is called an sequence

Example:- { 1, 3, 5, 7, 9, ..........}

and it is denoted by <
`a_(n)`

series:-

The sum of the sequence is called a series and it is denoted by

`S_(n)`

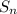
The gives series is geometric series 8,-24,72,.......

here a=8 and the ratio r=
`(a_(2) )/(a_(1) )`

`r= -3`

Step 2:-

Find The fourth term of the given sequence

Given a=8 and r= -3

`t_(n)= a r^(n-1)`

`t_(4) = 8(-3)^(4-1)`

`t_(4)=8(-3)^3= -216`

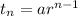
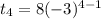
Find The fifth term of the given sequence

Given a=8 and r= -3

`t_(n)=a r^(n-1)`

`t_(5) = 8(-3)^(5-1)`

`t_(5)=8(-3)^4= 648`

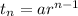
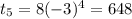
Step 3:-

now the geometric sequence 8,-24,72,-216,648

sum of the geometric sequence is called geometric series

The first five terms of geometric series

`S_(5) } = 8 -24+72-216+648=488`

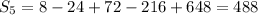
or

By using sum of the Geometric series formula

`S_(n) =(a(1-r^(n)) )/(1-r)  if  r < 1`

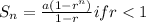
here a=8 and r = -3 <1

`S_(5) = (8(1-(-3)^5)/(1-(-3)) = 488`