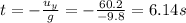Answer:
6.14 s
Step-by-step explanation:
The time the rocket takes to reach the top is only determined from its vertical motion.
The initial vertical velocity of the rocket is:
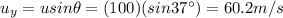
where
u = 100 m/s is the initial speed
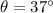 is the angle of launch
is the angle of launch
Now we can apply the suvat equation for an object in free-fall:
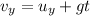
where
 is the vertical velocity at time t
is the vertical velocity at time t
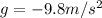 is the acceleration of gravity
is the acceleration of gravity
The rocket reaches the top when

So by substituting into the equation, we find the time t at which this happens: