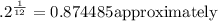Answer:
1) 20%
2) Choice a.
Explanation:
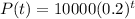
1)
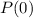 is the population initially.
is the population initially.
 is the population after a year.
is the population after a year.
 represents the population increase factor.
represents the population increase factor.
So let's evaluate that fraction:

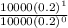
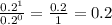
0.2=20%
2) Let's figure out the population growth in terms of months instead of years.
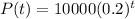
We want t to represent months.
A full year is 12 months, in a full year we have that
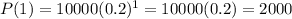
So we want a new P such that
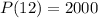 since 12 months equals a year.
since 12 months equals a year.
Let's look at the functions given to see which gives us this:
a)
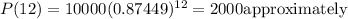
b)
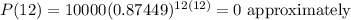
c)
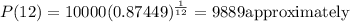
d)
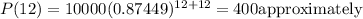
So a is the function we want.
Also another way to look at this:
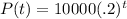 where
where
 is in years.
is in years.
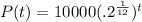 where
where
 is in months.
is in months.
And