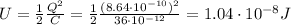Question

A capacitor consists of two parallel metal plates in air. The distance between the plates is

5.00 mm and the capacitance is 72 pF. The potential difference between the plates is raised to 12.0 V
with a battery
(a) Calculate the energy stored in the capacitor.
* (b) The battery is then disconnected from the capacitor; the capacitor retains its charge. Calculate the
energy stored in the capacitor if the distance between the plates is increased to 10.0 mm.

Answer 1

(a)
`5.18\cdot 10^(-9) J`

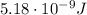
The energy stored in a capacitor is given by:

`U=(1)/(2)CV^2`

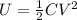
where

C is the capacitance

V is the potential difference between the plates

For the capacitor in this problem,

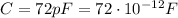`C=72 pF = 72\cdot 10^(-12) F` is the capacitance

V = 12.0 V is the potential difference across the plate

Substituting into the equation, we find

`U=(1)/(2)(72\cdot 10^(-12))(12.0)^2=5.18\cdot 10^(-9) J`

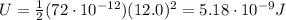
(b)
`1.04\cdot 10^(-8)J`

For this part, we have to calculate the charge stored on the capacitor first. This is given by

`Q=CV`

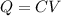
And substituting the values of C and V from the previous part, we find

`Q=(72\cdot 10^(-12))(12.0)=8.64\cdot 10^(-10) C`

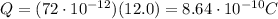
Now, in this second part, the battery is disconnected and the charge does not change. However, the capacitance of the capacitor changes; in fact, it is given by

`C=(\epsilon_0 A)/(d)`

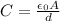
where

`\epsilon_0` is the vacuum permittivity, A the area of the plates, d their separation. Here the distance between the plates is increased from 5.00 mm to 10.0 mm, so it is doubled: since C is inversely proportional to d, this means that the new capacitance is half of its original value:

`C'=(72)/(2)=36 pF = 36\cdot 10^(-12) F`

And now we can find the new energy stored with the equation:

`U=(1)/(2)(Q^2)/(C)=(1)/(2)((8.64\cdot 10^(-10))^2)/(36\cdot 10^(-12))=1.04\cdot 10^(-8)J`