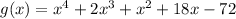Question

If a polynomial P has real coefficients, and if z = a + ib is a zero of P, then its conjugate z conjugate= a − ib is also a zero of P. (a) Given that x = 2 − 3 is a zero of P(x) = x ³ − 7x² + 25x − 39, find the other remaining zeros. (i) Find a polynomial of lowest degree with real coefficients and the given zeros: x = −1 and x = 1 − i (ii) x = 2, x = −4 and x = −3i.​

Answer 1

`\textsf{(a)} \quad x = 2+3i, \quad x=3`

`\textsf{(i)} \quad f(x)=x^3-x^2+2`

`\textsf{(ii)} \quad g(x)=x^4+2x^3+x^2+18x-72`

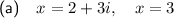
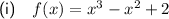
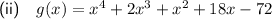
Explanation:

`\boxed{\begin{minipage}{3.6 cm}\underline{Imaginary number rule}\\\\$ \phantom{)))))))))}i^2=-1$\\ \end{minipage}}`

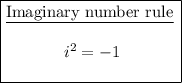
Part (a)

Given function:

`P(x)=x^3-7x^2+25x-39`

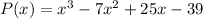
According to the Complex Conjugate Root Theorem, If x = (2 - 3i) is a zero of the given function, the complex conjugate x = (2 + 3i) must also be a zero.

`x=2-3i \implies (x-(2-3i))=0`

`x=2+3i \implies (x-(2+3i))=0`

`\begin{aligned}(x-(2-3i))(x-(2+3i)) & = x^2-(2+3i)x-(2-3i)x+(2-3i)(2+3i)\\ & = x^2-2x-3ix-2x+3ix+4+6i-6i-9i^2\\ & = x^2-4x+4-9(-1)\\ & = x^2-4x+13\end{aligned}`

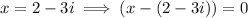
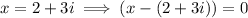
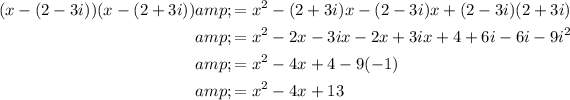
Therefore,
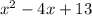`x^2-4x+13` is a factor of the given polynomial.

To find the other remaining zero:

`\begin{aligned}P(x) & =(x-a)(x^2-4x+13)\\& = x^3-4x^2+13x-ax^2+4ax-13a\\& = x^3-(4+a)x^2+(13+4a)x-13a\end{aligned}`

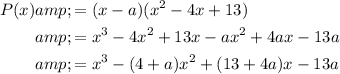
Compare the constant to that of the given function to find the value of a.

`\implies -13a=39 \implies a=3`

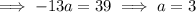
Therefore:

`P(a)=(x-3)(x^2-4x+13)`

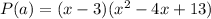
The zeros of the given function P(x) are:

• 
  `x = 2 - 3i`

• 
  `x = 2 + 3i`

• 
  `x = 3`

Part (i)

According to the Complex Conjugate Root Theorem, If x = (1 - i) is a zero of the given function, the complex conjugate x = (1 + i) must also be a zero. If x = -1 is also a zero, then:

`x=-1 \implies (x+1)=0`

`x=(1-i) \implies (x-(1-i))=0`

`x=(1+i) \implies (x-(1+i))=0`

Therefore:

`\begin{aligned}f(x) & =(x+1)(x-(1-i))(x-(1+i))\\& = (x+1)(x^2-(1+i)x-(1-i)x+(1-i)(1+i))\\ & = (x+1)(x^2-x-ix-x+ix+1+i-i-i^2\\&=(x+1)(x^2-2x+1-(-1))\\&=(x+1)(x^2-2x+2)\\& = x^3-2x^2+2x+x^2-2x+2\\& = x^3-x^2+2\end{aligned}`

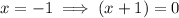
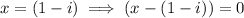
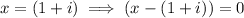
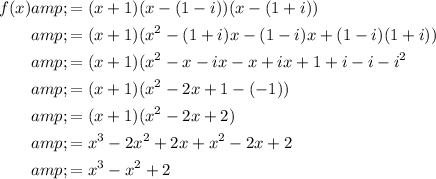
Therefore, a polynomial of the lowest degree with real coefficients and the given zeros is:

`f(x)=x^3-x^2+2`

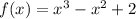
Part (ii)

According to the Complex Conjugate Root Theorem, If x = -3i is a zero of the given function, the complex conjugate x = 3i must also be a zero. If x = 2 and x = -4 are also zeros, then:

`x=2 \implies (x-2)=0`

`x=-4 \implies (x+4)=0`

`x=-3i \implies (x+3i)=0`

`x=3i \implies (x-3i)=0`

Therefore:

`\begin{aligned}g(x) & =(x-2)(x+4)(x+3i)(x-3i)\\& = (x^2+4x-2x-8)(x^2-3ix+3ix-9i^2)\\&=(x^2+2x-8)(x^2-9(-1))\\&=(x^2+2x-8)(x^2+9)\\& = x^4+9x^2+2x^3+18x-8x^2-72\\& = x^4+2x^3+x^2+18x-72\end{aligned}`

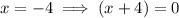
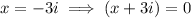
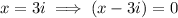
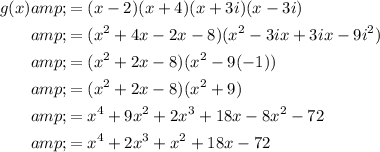
Therefore, a polynomial of the lowest degree with real coefficients and the given zeros is:

`g(x)=x^4+2x^3+x^2+18x-72`