Question

What should I buy? A study conducted by a research group in a recent year reported that 57% of cell phone owners used their phones inside a store for guidance on purchasing decisions. A sample of 14 cell phone owners is studied. Round the answers to at least four decimal places. Part 1 of 4 Your Answer is incorrect (a) What is the probability that seven or more of them used their phones for guidance on purchasing decisions? The probability that seven or more of them used their phones for guidance on purchasing decisions is 0.211.

Answer 1

Hence, the probability that seven or more of them used their phones for guidance on purchasing decisions is 0.7887

Explanation:

We are given the following information in the question:

We treat people using phones in the store for guidance as a success.

P(People use phone for guidance) = 57% = 0.57

Then the number of people follows a binomial distribution, where

Formula:

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 14 and x = 7

We have to evaluate:

`P(x \geq 7) = P(x = 7) + P(x = 8) + P(x = 9) + P(x = 10) + P(x =11) + P(x = 12) + P(x = 13) + P(x = 14)\\= \binom{14}{7}(0.57)^7(1-0.57)^7 + \binom{14}{8}(0.57)^8(1-0.57)^6 + \binom{14}{7}(0.57)^9(1-0.57)^5 + \binom{14}{7}(0.57)^(10)(1-0.57)^4 + \binom{14}{7}(0.57)^(11)(1-0.79)^3 + \binom{14}{7}(0.57)^(12)(1-0.57)^2 + \binom{14}{7}(0.57)^(13)(1-0.57)^1 + \binom{14}{7}(0.57)^(14)(1-0.57)^0\\= 0.7887 = 78.67\%`

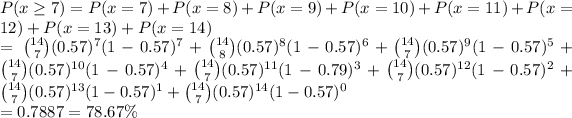
Hence, the probability that seven or more of them used their phones for guidance on purchasing decisions is 0.7887