Answer:
The total number of moles of gas in the mixture is 0.16939.
1.25550 grams of methane gas and 3.18848 grams of oxygen gas.
Step-by-step explanation:
Total volume of the mixture = V = 10.5 L
Temperature of the mixture = T = 35°C = 308.15K
Pressure of the mixture = P
Total moles of mixture = n =
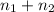
Using an ideal gas equation :
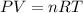
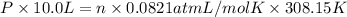
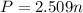
Partial pressure of the methane=
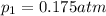
Moles of the methane=

Partial pressure of the oxygen gas=

Moles of the methane=
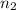
Mole fraction of the methane=
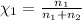
Mole fraction of the oxygen gas=
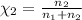
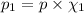 (Dalton's law)
(Dalton's law)
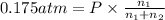
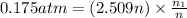

Mass of 0.06975 moles of methane gas :
0.06975 mol × 18 g/mol =1.25550 g
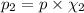 (Dalton's law)
(Dalton's law)
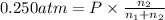


Mass of 0.06975 moles of oxygen gas :
0.09964 mol × 32 g/mol =3.18848 g
Total moles of mixture = n =
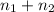
[/tex]=0.06975 mol+0.09964 mol=0.16939 mol[/tex]