Question

An initially stationary box of sand is to be pulled across a floor by means of a cable in which the tension should not exceed 1130 N. The coefficient of static friction between the box and the floor is 0.430. (a) What should be the angle between the cable and the horizontal in order to pull the greatest possible amount of sand, and (b) what is the weight of the sand and box in that situation?

Answer 1

solved

Step-by-step explanation:

According to the question

T= 1130 N

N = m*g - T*sin(θ)

f= µN

Therefore frictional force f = µ*(m*g - 1130*sin(θ))

So the forces in the horizontal are T*cos(θ) - f = 0

1100*cos(θ) = µ*(m*g - 1100*sin(θ))

cos(θ) + µ×sin(θ) = µ×m×g/1100

to find the angle for maximum mass take the derivative of mass with respect to θ and set it to 0

So -sin(θ)*dθ + µ*cos(θ)*dθ = µ*g/1100*dm

so -sin(θ) + µ*cos(θ) = µ*g/1100*dm/dθ = 0

So sin(θ) = µ*cos(θ)

So tan(θ) = µ

therefore,
`\theta= tan^(-1)(\mu)`

`\theta= tan^(-1)(0.430)`

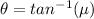
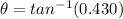
θ= 23.26°

b)Now using cos(θ) + µ×sin(θ) = µ×m×g/1130

we solve for m×g = W

W = 1100×(cos(θ) + µ×sin(θ))/(µ) = 1130×(cos(23.26) + 0.430×sin(23.26))/(0.430) = 1038.55 N