Question

Your coin collection contains 95 1952 silver dollars. If your grandparents purchased them for their face value when they were new, how much will your collection be worth when you retire in 2060, assuming they appreciate at an annual rate of 4.9 percent? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.)

Answer 1

Value of collection = $16,652.38

Step-by-step explanation:

The compound interest formula is:

`A=P[1+(r)/(n) ]^(nt)`

where,

P is the principal, which is $95 since that is the original value of 95 silver dollars purchase for $1 each.

r is the interest rate of 4.9%, expressed as 0.049

n is the number of times interest compounds each year, which is 1

t is the number of years the money is invested, which is 108 because we are calculating the gain between 1952 and 2060

Plug that in, and we get:

`A=95[1+(0.049)/(1) ]^(108)`

`A=95(1.049)^(108)`

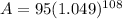
A = 95 × 175.2882

A = $16,652.38

Therefore,

Value of collection = $16,652.38