Question

A solid lies between planes perpendicular to the x-axis at x tox=. The cross sections perpendicular to the x-axis are circular disks with diameters running from the curve y cotx to the curve y csc x.

Find the volume of the solid.
A. +1) OA 6 2 O
B. (2/3-2)-3 n2 O
C. (3-1)x+ (3-1)
D. 2 12

Answer 1

It's unclear what the planes are supposed to be, so I'll take
`x=a` and
`x=b` with
`0\le a<b<\pi`.

The cross sections are disks with diameter
`\csc x-\cot x`, so each disk of thickness
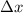`\Delta x` has a volume of

`\frac{\pi(\csc x-\cot x)^2}4\Delta x`

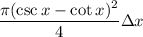
Then taking infinitesimally thin disks, we find the solid has a volume of

`\displaystyle\frac\pi4\int_a^b(\csc x-\cot x)^2\,\mathrm dx`

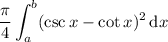
Since

`(\csc x-\cot x)^2=2\csc^2x-2\csc x\cot x-1`

and

`(\mathrm d(\csc x))/(\mathrm dx)=-\csc x\cot x`

`(\mathrm d(\cot x))/(\mathrm dx)=-\csc^2x`

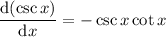
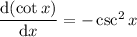
it follows that the volume is

`\displaystyle\frac\pi4\left(-2\cot x+2\csc x-x\right)\bigg|_a^b`

`=\frac\pi4(2(\cot a-\cot b)+2(\csc b-\csc a)+a-b)`

`=\frac\pi4\left(2\tan\frac b2-2\tan\frac a2+a-b\right)`