Question

Use the drawing tool(s) to form the correct answer on the provided number line.

Consider the given function.

f(x) = x^3 - 2x^2 - 11x + 12

Use the remainder theorem to find the x-intercepts of the function, and plot their x-values on the number line.

Answer 1

x= 1, x= 4, and x= -3

Explanation:

Use the possible combinations of factors of the constant term of the polynomial to find a first root. Try 1, -1, 2, -2, 3, -3, etc.

Notice in particular that x = 1 is a root (makes f(1) = 0):

`f(1)=x^3-2*1^2-11*1+12=1-2-11+12=13-13=0`

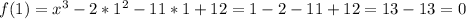
So we know that x=1 is a root, and therefore, the binomial (x-1) must divide the original polynomial exactly.

As we perform the division, we find that the remainder of it is zero (perfect division) and the quotient is:
`x^2-x-12`

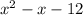
This is now a quadratic expression for which we can find its factor form:

`x^2-x-12=x^2-4x+3x-12=x(x-4)+3(x-4)=(x-4)*(x+3)`

From the factors we just found, we conclude that x intercepts (zeroes) of the original polynomial are those x-values for which each of the factors: (x-1), (x-4) and (x+3) give zero. That is, the values x= 1, x= 4, and x= -3. (these are the roots of the polynomial.

Mark these values on the number line as requested.