Answer: Choice B
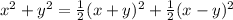
===================================================
Step-by-step explanation:
Let's go through the answer choices to see which are true and which are false.
------------------------
Choice A is false because it should be
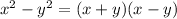
which is the difference of squares factoring rule.
However, the left hand side of choice A has a plus, and not a minus.
Consequently, this rules out choice D.
------------------------
Choice B is true
We can conclude this by eliminating the other answer choices as false, and by noticing the following:
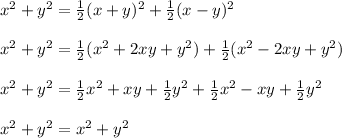
This confirms why choice B is an identity. The equation is true for any real numbers x and y.
Let's look at an example. I'll pick x = 4 and y = 7

I'll let you try other (x,y) pairs of values. Keep in mind that using numeric examples like this is not a proof. The proof would be using algebra to expand and simplify the right hand side so it becomes the left hand side.
------------------------
Choice C is false. The right hand side
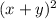 expands out to
expands out to

A common mistake students do is to forget about the 2xy when expanding out
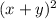 , which may lead to choice C being a slight trick answer.
, which may lead to choice C being a slight trick answer.
If choice C said
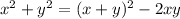 , then we'd have a true identity
, then we'd have a true identity
------------------------
Choice D is false. Refer to the formula I wrote in choice A.