Question

A profit -maximizing firm has the total-cost function c= x^2 + 2x and sells into a competitive market on which the price is $10. what output should it produce?

hint: Find the derivative and check for local maxima and minima

Answer 1

The output produce is 4.

Explanation:

Given : A profit -maximizing firm has the total-cost function
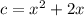`c= x^2+2x` and sells into a competitive market on which the price is $10.

To find : What output should it produce?

Solution :

The total-cost function
`C(x)= x^2+2x`

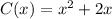
The revenue function is price into number of item,

So, The revenue function is
`R(x)=10x`

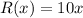
The profit function is given by,

`P(x)=R(x)-C(x)`

`P(x)=10x-(x^2+2x)`

`P(x)=10x-x^2-2x`

`P(x)=8x-x^2`

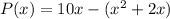
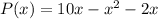
The derivative of the profit function,

`P'(x)=8-2x`

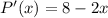
Equate it to zero to get output,

`8-2x=0`

`2x=8`

`x=4`

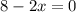
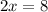
For maxima/minima we find the second derivative,

`P''(x)=-2`

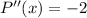
As
`c''(x)<0` it is a local maxima.

Therefore, The output produce is 4.