Question

6. Prove that if 3n^3+13 is odd then n is even for all integers n, using the proof by contradiction.

Answer 1

If 3n^3+13 is odd then n is even for all integers n, using the proof by contradiction.

Explanation:

By contradiction method, we need to prove that if
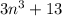`3n^3+13` is odd then n is even for all integers n.

Proof by contradiction:

Let as assume if
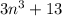`3n^3+13` is odd then n is odd for all integers n.

`n=2k+1`

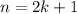
Substitute the value of n in the given expression.

`3(2k+1)^3+13`

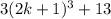
Cube of any odd number is an odd number.

`(2k+1)^3=Odd`

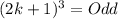
Product of two odd numbers is an odd number.

`3(2k+1)^3=Odd`

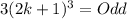
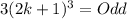`3(2k+1)^3=Odd` is an odd number and 13 is an odd number. We know that addition of two odd numbers is an even number.

`3(2k+1)^3+13=Even`

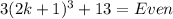
Which is the contradiction of our assumption.

If 3n^3+13 is odd then n is even for all integers n, using the proof by contradiction.

Hence proved.