Question

A 17.5 kg block is dragged over a rough, horizontal surface by a constant force of 167 N acting at an angle of 30◦ above the horizontal. The block is displaced 23.9 m, and the coefficient of kinetic friction is 0.136. The acceleration of gravity is 9.8 m/s 2 . 17.5 kg µ = 0.136 167 N 30 ◦ If the block was originally at rest, determine its final speed. Answer in units of m/s.

Answer 1

`v = 19.03 m/s`

Step-by-step explanation:

As we know that the block is dragged over the surface by external force at an angle of 30 degree above the horizontal

Now we will have

`F_n + F sin30 = mg`

`F_n = mg - F sin30`

`F_n = 17.5(9.81) - 167 sin30`

`F_n = 88.175 N`

now we know that net horizontal force on the block is given as

`F_x = Fcos30 - F_f`

`F_x = 167 cos30 - \mu F_n`

`F_x = 167cos30 - 0.136(88.175)`

`F_x = 132.6 N`

now we know that

work done by net force is equal to change in kinetic energy of the block

so we have

`F_x . d = (1)/(2)mv^2 - 0`

`132.6 * 23.9 = (1)/(2)(17.5) v^2`

`v = 19.03 m/s`

Answer 2

The final velocity of the block is 68.85m/s.

Step-by-step explanation:

The final velocity can be determined by means of the equations for a Uniformly Accelerated Rectilinear Motion:

`v_(f)^(2) = v_(i)^(2) + 2ad`

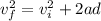
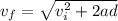`v_(f) = \sqrt{v_(i)^(2) + 2ad}` (1)

But it is necessary to know the acceleration. For a better procedure it will be listed the knowns and unknowns of the problem:

Knowns:

F = 167 N

`\theta` = 30°

m = 1.75 Kg

d = 23.9 m

`\mu` = 0.136

Unknowns:

`F_(r)` = ?

a = ?

The acceleration can be found by means of Newton's second law:

`\sum F_(net) = ma`

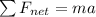
Where
`\sum F_(net)` is the net force, m is the mass and a is the acceleration.

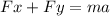`Fx + Fy = ma` (2)

All the forces can be easily represented in a free body diagram, as it is shown below.

Force in the x axis:

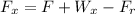`F_(x) = F + W_(x) - F_(r)` (3)

Forces in the y axis:

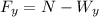`F_(y) = N - W_(y)` (4)

Solving for the forces in the x axis:

`F_(x) = F + W_(x) - F_(r)`

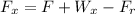
Notice that is necessary to found
`F_(r)`:

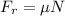`F_(r) = \mu N` (5)

The normal force can be obtained from equation (4)

`N - W_(y) = 0`

`N = W_(y)`

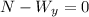
The component of the weight in the y axis can be gotten by means of trigonometry:

`(Adjacent)/(Hypotenuse) = cos \theta`

`(W_(y))/(W) = cos \theta`

`W_(y)= W cos \theta`

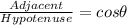
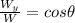
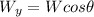
Remember that the weight is defined as:

`W = mg`

`W_(y)= mgcos \theta`

`N = mg cos \theta`

`F_(r) = \mu mgcos \theta`

`F_(r) = (0.136)(1.75Kg)(9.8m/s^(2))(cos30)`

`F_(r) = 2.01N`

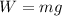
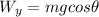
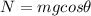
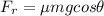
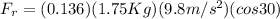
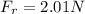
The component of the weight in the x axis can be gotten by means of trigonometry:

`(Opposite)/(Hypotenuse) = sen \theta`

`(W_(x))/(W) = sen \theta`

`W_(x) = W sen \theta`

`W_(x) = mgsen \theta`

`W_(x) = (1.75Kg)(9.8m/s^2)(sen30)`

`W_(x) = 8.57N`

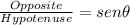
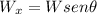
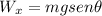
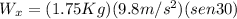
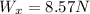
Then, replacing
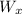`W_(x)` and
`F_(r)` in equation (3) it is gotten:

`F_(x) = 167N + 8.57N - 2.01N`

`F_(x) = 173.56N`

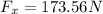
Solving for the forces in the y axis:

`F_(y) = N - W_(y)`

`F_(y) = mgcos \theta - mgcos \theta`

`F_(y) = 0`

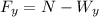
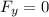
Replacing the values of
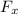`F_(x)` and
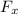`F_(x)` in equation (2) it is gotten:

`F_(x) + 0 = ma`

`F_(x) = ma`

`a = (F_(x))/(m)`

`a = (173.56N)/(1.75Kg)`

`a = (173.56Kg.m/s^(2))/(1.75Kg)`

`a = 99.17m/s^(2)`

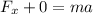
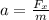
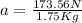
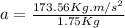
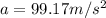
Now that the acceleration is known, equation (1) can be used:

`v_(f) = \sqrt{v_(i)^(2) + 2ad}`

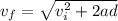
However, since the block was originally at rest its initial velocity will be zero (
`v_(i) = 0`).

`v_(f) = √(2ad)`

`v_(f) = \sqrt{2(99.17m/s^(2))(23.9m)}`

`v_(f) = \sqrt{2(99.17m/s^(2))(23.9m)}`

`v_(f) = 68.85m/s`

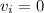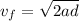
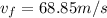
Hence, the final velocity of the block is 68.85m/s.