Question

What is the area of a triangle with vertices at (0, – 2), (8, – 2), and (9, 1)?

Enter your answer in the box.
units2

Answer 1

Answer: 12

Explanation:

Just did the test

Answer 2

The area of the triangle with vertices at (0, – 2), (8, – 2), and (9, 1) is 12 square units.

SOLUTION:

Given, vertices of the triangle are A(0, -2), B(8, -2) and C(9, 1).

We have to find the area of the given triangle.

We know that,

`\text { Area of triangle }=(1)/(2)\left(x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right)`

`\text { Where, }\left(x_(1), y_(1)\right),\left(x_(2), y_(2)\right),\left(x_(3), y_(3)\right) \text { are vertices of the triangle. }`

Here in our problem,
`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right)=(0,-2),\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)=(8,-2) \text { and }\left(\mathrm{x}_(3), \mathrm{y}_(3)\right)=(9,1)`

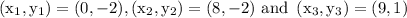
Now, substitute the above values in the formula.

`\text { Area of triangle }=(1)/(2)\left(x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right)`

`=(1)/(2)(0(-2-1)+8(1-(-2))+9(-2-(-2))`

`=(1)/(2)(0+8(1+2)+9(2-2))`

`(1)/(2)(0 + 0 +24) = (24)/(12) = 2`

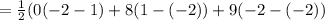
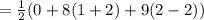
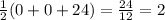
Hence, the area of the triangle is 12 sq units.