Question

Can someone explain to me how to find the vertex form of this equation? y= -x^2 + 12x-4

Answer 1

The vertex of given equation
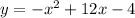`y=-x^(2)+12 x-4` is (6, 32).

SOLUTION:

Given, quadratic equation is
`y=-x^(2)+12 x-4`

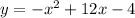
Above equation is a parabola and we need to find the vertex of that parabola. We know that, general form of the parabola is
`y=a(x-h)^(2)+k`

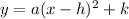
Where, (h, k) is the vertex.

So, let us convert the given equation in parabolic equation.

`\begin{array}{l}{y=-x^(2)+12 x-4} \\ {y=-\left(x^(2)-12 x+4\right)} \\ {y=-\left(x^(2)-(2)(x)(6)+6^(2)-6^(2)+4\right)} \\ {\left.y=-\left((x-6)^(2)-36+4\right)\right)} \\ {y=-(x-6)^(2)+32}\end{array}`

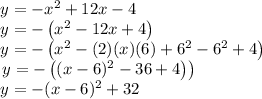
Now, by comparing above equation with general form,

h = 6, k = 32 and a = -1.

Hence, the vertex of given equation is (6, 32).