Answer: 37.981 m/s
Step-by-step explanation:
This situation is related to projectile motion or parabolic motion, in which the travel of the ball has two components: x-component and y-component. Being their main equations as follows:
x-component:
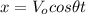 (1)
(1)
Where:
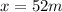 is the point where the ball strikes ground horizontally
is the point where the ball strikes ground horizontally
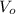 is the ball's initial speed
is the ball's initial speed
 because we are told the ball is thrown horizontally
because we are told the ball is thrown horizontally
 is the time since the ball is thrown until it hits the ground
is the time since the ball is thrown until it hits the ground
y-component:
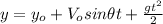 (2)
(2)
Where:
 is the initial height of the ball
is the initial height of the ball
 is the final height of the ball (when it finally hits the ground)
is the final height of the ball (when it finally hits the ground)
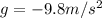 is the acceleration due gravity
is the acceleration due gravity
Knowing this, let's start by finding
 from (2):
from (2):
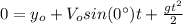 (3)
(3)

 (4)
(4)
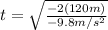 (5)
(5)
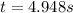 (6)
(6)
Then, we have to substitute (6) in (1):
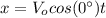 (7)
(7)
And find
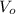 :
:
 (8)
(8)
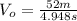 (9)
(9)
 (10)
(10)
On the other hand, since we are dealing with constant acceleration (due gravity) we can use the following equation to find the value of the ball's final velocity
 :
:
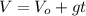 (11)
(11)
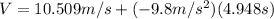 (12)
(12)
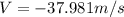 (13) This is the ball's final velocity, and the negative sign indicates its direction is downwards.
(13) This is the ball's final velocity, and the negative sign indicates its direction is downwards.
However, we were asked to find the ball's final speed, which is the module of the ball's final vleocity vector. This module is always positive, hence the speed of the ball just before it strikes the ground is 37.981 m/s (positive).