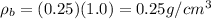Answer:
A 0.25 g/cm3
Step-by-step explanation:
At equilibrium, the buoyant force acting on the block (B, upward) is equal to its weight (W, downward):
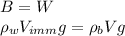
where
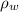 is the water density
is the water density
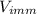 is the part of the volume of the block immersed in the water
is the part of the volume of the block immersed in the water
g is the acceleration of gravity
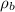 is the density of the block
is the density of the block
V is the volume of the block
Re-arranging the equation,
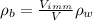
where we know:
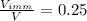 , since the fraction of volume immersed is 25%
, since the fraction of volume immersed is 25%
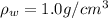
Substituting,