Question

(d) You observe someone pulling a block of mass 41 kg across a low-friction surface. While they pull a distance of 4 m in the direction of motion, the speed of the block changes from 5 m/s to 7 m/s. Calculate the magnitude of the force exerted by the person on the block.

Answer 1

The magnitude of the force is 124.23 N.

Step-by-step explanation:

To known the magnitude of the force is necessary to find the acceleration, that can be done by means of the equations for a a Uniformly Accelerated Motion:

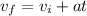`v_(f) = v_(i) + at` (1)

Where
`v_(f)` is the final velocity,
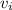`v_(i)` is the initial velocity, a is the acceleration and t is the time.

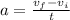`a = (v_(f)-v_(i))/(t)` (2)

`d = v_(i)t + (1)/(2)at^(2)` (3)

By replacing (2) in equation (3) it is gotten:

`d = v_(i)t + (1)/(2)((v_(f)-v_(i))/(t))t^(2)`

`d = v_(i)t + (1)/(2)(v_(f)-v_(i))t`

`d = v_(i)t + (1)/(2)v_(f)t-(1)/(2)v_(i)t`

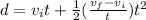
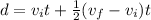
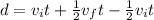
Therefore, by subtracting the first and third term (
`v_(i)t-(1)/(2)v_(i)t` ⇒
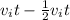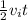`(1)/(2)v_(i)t`) it is got:

`d = (1)/(2)v_(f)t + (1)/(2)v_(i)t`

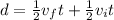
Applying common factor for
`(1)/(2)t`:

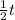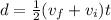`d = (1)/(2)(v_(f) + v_(i))t` (4)

Equation (4) can be rewritten in terms of t:

`t = (2d)/((v_(f) + v_(i)))`

`t = ((2)(4m))/((7m/s + 5m/s))`

`t = (8m)/(12m/s)`

`t = 0.66s`

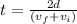
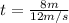
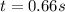
By knowing the time is possible to determine the acceleration by means of equation (2):

`a = (7m/s-5m/s)/(0.66s)`

`a = (2m/s)/(0.66s)`

`a = 3.03m/s^(2)`

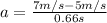
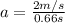
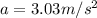
The magnitude of the force exerted by the person on the block can be determine by means of Newton's second law:

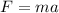`F = ma` (5)

`F = (41Kg)(3.03m/s^(2))`

`F = 124.23 Kg.m/s^(2)`

`F = 124.23 N`

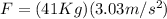
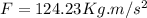
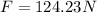
Hence, the magnitude of the force is 124.23 N.