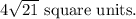ANSWER:
The area of the triangle with sides a=5, b=8 and c=11 is
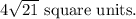
SOLUTION:
Given, a = 5, b = 8, c = 11.
We need to find the area of the triangle with sides as given.
Let us find the area of triangle using heron’s formula:
![\begin{array}{l}{\text { Area }=\sqrt[2]{s(s-a)(s-b)(s-c)}} \\\\ {\text { Where } s=(a+b+c)/(2)}\end{array}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/upuqdc9685crzwlpy0hw2hrne8tuqy6l7h.png)
Now, let us calculate value of s and put it in heron’s formula.
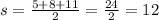
Substitute s value in heron’s formula along with a, b, c values.
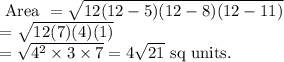
Thus the area of the triangle with sides a=5, b=8 and c=11 is