Question

15. Construct the slope-intercept form equation of the line passing through (-5,23) and (10,-5).

Equation:

Answer 1

15y = -28 x + 205.

Explanation:

Slope intercept form of equation is y = mx + c where m is slope and c is the y intercept.

Now slope of line passing through points (-5, 23) and (10, -5):

`m = (y_(2) - y_(1) )/(x_(2) - x_(1) ) = (-5 -23)/(10 + 5) = (-28)/(15)`

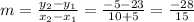
Now equation of line:

y = mx + c

substituting the value of m in above expression,

`y = -(28)/(15) x + c`

Now, since the line is passing through the point (-5, 23) therefore, x = -5 and y = 23. By substituting these values in above equation,

`23 = -(28)/(15) * (-5) + c`

`23 = (28)/(3) + c`

`c = 23 - (28)/(3) = (69 - 28)/(3) = (41)/(3)`

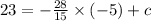
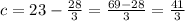
So equation of line in slope intercept form:

`y = -(28)/(15) x + (41)/(3)`

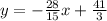
Further solving,

15y = -28 x + 205.