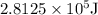The work done is
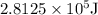
Work Done = Change in Kinetic Energy (ΔKE)
Step-by-step explanation
In first 1 hour it travels 72 km
So, Velocity =
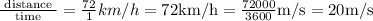
or, Initial Velocity (u) = 20 m/s
Similarly for the next hour it covers 90 km
So, Velocity =
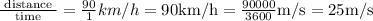
or, Final Velocity (v) = 20 m/s
Work done = Change in Kinetic Energy (ΔKE)
Work done = ΔKE =

ΔKE =
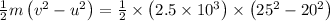
=
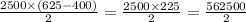 = 281250 joule
= 281250 joule
=