1 Answer

Ayman El Temsahi · Answer 1 · 2020-09-11T17:20:53+0000

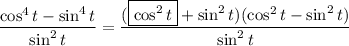
$(\cos^4t-\sin^4t)/(\sin^2t)=\frac{(\boxed{\cos^2t}+\sin^2t)(\cos^2t-\sin^2t)}{\sin^2t}$

which follows from the difference-of-squares identity,
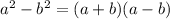a^2-b^2=(a+b)(a-b) , with
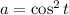$a=\cos^2t$ and
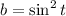$b=\sin^2t$ .

$=\frac{(\boxed{1})(\cos^2t-\sin^2t)}{\sin^2t}$

which is due to the Pythagorean identity.

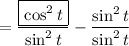
$=\frac{\boxed{\cos^2t}}{\sin^2t}-(\sin^2t)/(\sin^2t)$

by the distributive property;
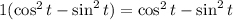$1(\cos^2t-\sin^2t)=\cos^2t-\sin^2t$ .

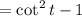
$=\cot^2t-1$

by definition of cotangent,
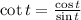$\cot t=(\cos t)/(\sin t)$ .

$(\cos^2\theta)/(1-\sin\theta)=\frac{1-\boxed{\sin^2\theta}}{1-\sin\theta}$

due to the Pythagorean identity.

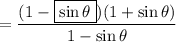
$=\frac{(1-\boxed{\sin\theta})(1+\sin\theta)}{1-\sin\theta}$

by factorization of the numerator as a difference of squares.

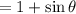
$=1+\sin\theta$

by cancellation of
$1-\sin\theta$ (provided
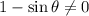$1-\sin\theta\\eq0$ ).

Please log in or register to add a comment.