Question

On a low-friction track, a 0.81 kg cart initially going at 1.85 m/s to the right collides with a cart of unknown inertia initially going at 2.17 m/s to the left. After the collision, the 0.81 kg cart is going at 1.32 m/s to the left, and the cart of unknown inertia is going at 3.22 m/s to the right. The collision lasts for 0.010 s.

Answer 1

The mass of unknown inertia is 0.476 kg.

Step-by-step explanation:

It is given that,

Mass of the cart, m₁ = 0.81 kg

Initial speed of cart, u₁ = 1.85 m/s (in right)

Initial speed of the other object, u₂ = -2.17 m/s (in left)

After the collision,

Final speed of the cart, v₁ = -1.32 m/s (in left)

Final speed of the other object, v₂ = 3.22 m/s (in right)

Let m₂ is the mass of the unknown inertia. Using the conservation of linear momentum to find the mass of unknown inertia.

`m_1u_1+m_2u_2=m_1v_1+m_2v_2`

`0.81* 1.85+m_2* (-2.17)=0.81* (-1.32)+m_2* 3.22`

`0.81* 1.85+0.81* 1.32=(3.22+2.17)m_2`

`m_2=(2.567)/(5.39)`

`m_2=0.476\ kg`

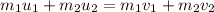
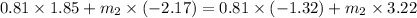
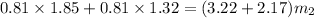
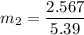
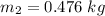
So, the mass of the unknown inertia is 0.476 kg. Hence, this is the required solution.