Answer:
a) The critical points are
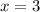 and
and
 .
.
b) f is decreasing in the interval
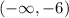
f is increasing in the intervals
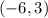 and
and
 .
.
c) Local minima:

Local maxima: No local maxima
Explanation:
(a) what are the critical points of f?
The critical points of f are those in which
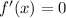 . So
. So
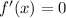

So, the critical points are
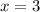 and
and
 .
.
(b) on what intervals is f increasing or decreasing? (if there is no interval put no interval)
For any interval, if
 is positive, f is increasing in the interval. If it is negative, f is decreasing in the interval.
is positive, f is increasing in the interval. If it is negative, f is decreasing in the interval.
Our critical points are
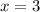 and
and
 . So we have those following intervals:
. So we have those following intervals:
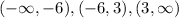
We select a point x in each interval, and calculate
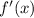 .
.
So
-------------------------
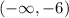
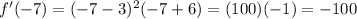
f is decreasing in the interval
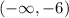
---------------------------
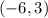
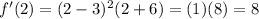
f is increasing in the interval
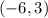 .
.
------------------------------
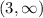

f is increasing in the interval
 .
.
(c) At what points, if any, does f assume local maximum and minima values. ( if there is no local maxima put mo local maxima) if there is no local minima put no local minima
At a critical point x, if the function goes from decreasing to increasing, it is a local minima. And if the function goes from increasing to decreasing, it is a local maxima.
So, for each critical point is this problem:
At
 , f goes from decreasing to increasing.
, f goes from decreasing to increasing.
So
 , f assume a local minima value
, f assume a local minima value
At
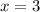 , f goes from increasing to increasing. So, there it is not a local maxima nor a local minima. So, there is no local maxima for this function.
, f goes from increasing to increasing. So, there it is not a local maxima nor a local minima. So, there is no local maxima for this function.