Question

The average of 5 numbers is 4 .

A sixth number is added to the set which increases the mean to 7 .What is the 6th number

Answer 1

The sixth number is 22. Surprisingly, the exact values of the first five numbers do not matter. See the explanation.

Explanation:

Let the sixth number be
`x`. The average of
`n` numbers is equal to the sum of these number divided by
`n`. That is:

`\displaystyle \text{Average} = \frac{\text{Sum of Entries}}{\text{Numbers of Entries}}`.

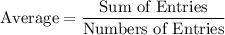Working backwards (multiply both sides by the denominator,
`n`) to find a formula for the sum of the numbers:

`\text{Sum of Entries} = n \cdot \text{Average of Entries}`.

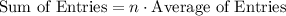Apply this formula to find the sum of the first five numbers:

`\underbrace{4}_{\text{Avg. of}\atop\text{entries}} * \underbrace{5}_{\text{Num. of}\atop \text{entries}} = 20`.

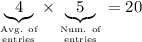If
`x` represents the value of the sixth number, the sum of the first six numbers will be equal to:

`20 + x`.

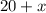The average of the first six number will thus be equal to:

`\displaystyle \text{Average of the first six numbers} = \frac{\text{Sum of Entries}}{\text{Numbers of Entries}}= (20 + x)/(6)`.

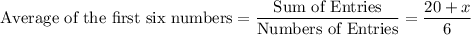However, the question states that the average of the first six numbers is equal to
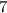`7`. In other words,

`\displaystyle (20 + x)/(6) = 7`.

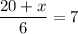Multiply both sides by the denominator,
`6`:

`20 + x = 42`.

`x = 22`.

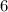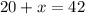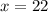In other words, the sixth number is
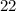`22`.