Question

A scooter travels 18 miles in the same time a bike covers 8 miles. If the rate of the scooter is two miles per hour than twice the rate of the bike, find both rates?

Answer 1

A scooter travels 18 miles in the same time a bike covers 8 miles.The rates of both scooter and bike are 8 miles per hour and 18 miles per hour

SOLUTION:

Given, a scooter travels 18 miles in the same time a bike covers 8 miles.

The rate of the scooter is two miles per hour than twice the rate of the bike

We need to find both rates of scooter and bike.

Let the speed of scooter be x and speed of bike be y.

And, time taken to travel be t.

Then, for scooter:

`\bold{distance = speed * time}`

`18 = x * t`

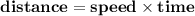
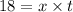
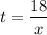`$t=(18)/(x)$` --- (1)

For bike:

`\bold{distance = speed * time}`

`$8=y * t$`

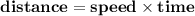
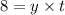
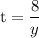`$\mathrm{t}=(8)/(y)$` --- (2)

Now, equate both (1) and (2)

`$(18)/(x)=(8)/(y)$`

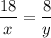
On cross-multiplication we get

18y = 8x

4x – 9y = 0 ---- (3)

We also know that, rate of the scooter is two miles per hour than twice the rate of the bike.

x = 2 + 2y ---- (4)

Now substitute (4) in (3)

4(2 + 2y) – 9y = 0

8 + 8y – 9y = 0

9y – 8y = 8

y = 8.

Again substitute y value in (4)

x = 2 + 2(8) = 2 + 16

x = 18.

Hence, the rates of both scooter and bike are 8 and 18 miles per hour