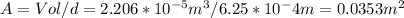Question

Suppose that a parallel-plate capacitor has a dielectric that breaks down if the electric field exceeds K V/m. Thus, the maximum voltage rating of the capacitor is Vmax=Kd, where d is the separation between the plates. In working problem P3.33, we find that the maximum energy that can be stored is wmax=12ϵrϵ0K2(Vol) in which Vol is the volume of the dielectric. Given that K = 32 × 105V/m and that ϵr = 1 (the approximate values for air), find the dimensions of a parallel-plate capacitor having square plates if it is desired to store 1 mJ at a voltage of 2000 V in the least possible volume.

Answer 1

The least possible volume is
`2.206*10^(-5) m^3`

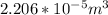
Step-by-step explanation:

We are asked by the least volume to store 1 mJ at 2000 V.

So, we can use the given formula for
`W_(max)` and solve for Vol.

`W_(max) = (1)/(2)\epsilon_r \epsilon_0 K^2 Vol\\Vol= 2W_(max)/(\epsilon_r \epsilon_0 K^2)`

replacing the values given in the problem and the permittivity of space
`\epsilon_0` which is
`8.854*10^(-12)F/m` we obtain Vol.

`Vol= 2*0.001 J/(1*8.854*10^(-12)F/m*(32*10^5V/m)^2)\\Vol= 0.002 J/( 90.66496F*V^2/m^3)\\Vol = 2.206*10^(-5) m^3`

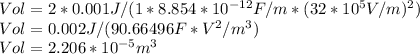
Note that
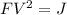`FV^2= J` in the above solution

Additional:

Taking into account that the volume of dieletric will be the area of plates (A) times the separation between plates (d).

`Vol=A*d`

You also can calculate A and d

d is calculated assuming that the
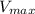`V_(max)` is 2000 V and using given equation for
`V_(max)`:

`d= V_(max)/K\\d= 2000V/(32*10^5V/m)\\d=6.25*10^-4 m`

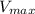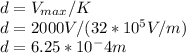
and A is calculated dividing Vol by d

`A= Vol/d=2.206*10^(-5) m^3/6.25*10^-4 m =0.0353 m^2`