Question

A hypothesis will be used to test that a population mean equals 10 against the alternative that the population mean is more than 10 with known Ï. What is the critical value of z-score for the following significance levels?

A) 0.01
B) 0.05
C) 0.10

Answer 1

A) 2.58

B) 1.96

C) 1.65

Explanation:

A hypothesis used to test that

`H_o : \mu  = 10`

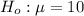
against the alternatives
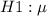`H1 : \mu` not equal to 10

if null hypothesis is true, then distribution of test statics follow

`Zo = (\bar x - \mu)/((\sigma)/(√(n)))`

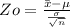
for two sided alternatives hypothesis
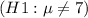`( H1: \mu \\eq 7)`, then P value is

`P = 2[1- \phi(\left | Zc \right |)]` (1)

a)significance level
`\alpha = 0.01`

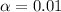
from 1 eq we get

`\pi (\left | Zc \right |) = P(Zo<\left | Zc \right |) = 1 - (0.01)/(2)  = 0.995`

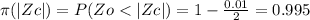
Therefore
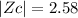`\left | Zc \right | = 2.58` FROM Z TABLE

B) significance level
`\alpha = 0.05`

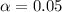
from 1st equation we get

`\pi (\left | Zc \right |) = P(Zo < \left | Zc \right |) = 1 - (0.05)/(2)  = 0.975`

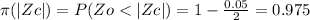
Therefore
`\left | Zc \right | = 1.96` FROM Z TABLE

C) significance level
`\alpha = 0.10`

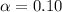
from 1 eq we get

`\pi (\left | Zc \right |) = P(Zo<\left | Zc \right |) = 1 - (0.10)/(2)  = 0.95`

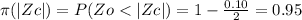
Therefore
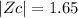`\left | Zc \right | = 1.65` FROM Z TABLE