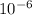Answer:
The capacite is C=5.32 uF using the equations of voltage and energy in capacitance
Step-by-step explanation:
The energy holds is 5 J and the resistor dissipates 2J so the energy total is 3J
Using:
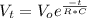
Voltage in this case is the energy dissipated so
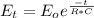
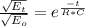
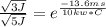
Using the equation to find capacitance
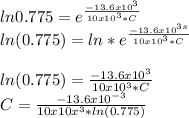
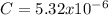 F
F
C= 5.32 uF because u is the symbol for micro that is equal to