Question

Mila had math and reading homework tonight. Mila can solve each math problem in 5 minutes and she can read each page in 2.5 minutes. Mila completed a total of 17 math problems and pages of reading in 55 minutes. Write a system of equations that could be used to determine the number of math problems Mila solved and the number of pages she read. Define the variables that you use to write the system.

Answer 1

Mila solved 5 math problems and read 12 pages in 55 minutes.

Explanation:

Let's call
`x` math problems and
`y` reading pages.

"MIla completed a tota of 17 math problem an pages of reading in 55 minutes", this expression can be model as

`x+y=17`

Which expresses the total number of homework made.

Mila can solve each math problem in 5 minutes, and she can read each page in 2.5 minutes. If all 17 problems took 55 minutes, we can elaborate a second relation about the time

`5x+2.5y=55`

So, we have the following system of equations

`\left \{ {{x+y=17} \atop {5x+2.5y=55}} \right.`

To solve this system, we are gonna multiply the first equation by -5 and then sum and solve for
`y`

`\left \{ {{-5x-5y=-85} \atop {5x+2.5y=55}} \right.\\-2.5y=-30\\y=(-30)/(-2.5)=12`

Then, we replace this value in one equation to get the other one

`x+y=17\\x+12=17\\x=17-12\\x=5`

Therefore, Mila solved 5 math problems and read 12 pages in 55 minutes.

Answer 2

Mila read 12 pages in 55 minutes. She solved 5 math problems in 55 minutes.

Explanation:

First, you must determine the unknown variables, these being:

• x: the number of math problems Mila solved.
• y: the number of pages Mila read.

Mila completed a total of 17 math problems and pages of reading. This means that the number of problems she solved plus the number of pages she read is 17. Expressed in an equation, this is: x+y=17 Equation (A)

On the other hand you know that Mila completed a total of 17 mathematical problems and reading pages is 55 minutes. And you know that Mila can solve every math problem in 5 minutes and she can read every page in 2.5 minutes. In other words, 5 times the amount of math problems is the amount of time it takes Mila to solve those problems. And 2.5 for each page read is the time it takes to read the "y" pages. And its sum is 55 minutes. So, expressed by an equation, this is: 5*x+2.5*y=55 Equation (B)

So, the system of equations is:

`\left \{ {{x+y=17} \atop {5*x+2.5*y=55}} \right.`

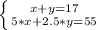
One of the most used and known methods for solving a system of equations is the substitution method. In this method, you isolate one of the variables from one of the equations and replace it in the other equation. In this case you can choose to isolate the variable "x" from equation (A), leaving the equation:

y=17 - x

Replacing in equation (B), you get:

5*(17-y)+2.5*y=55

Now you solve the equation, isolating the value of "y":

5*17-5*y+2.5*y=55

85-5*y+2.5*y=55

85-2.5*y=55

-2.5*y=55-85

-2.5*y=-30

Finally:

y=12

Remember that y is the number of pages Mila read, so this means that Mila read 12 pages in 55 minutes.

To easily find the value of the other variable, you can simply replace the value of "and" calculated in the previously isolated equation. So:

Remember that x=17 - y

Replacing the value of y: x=17 -12

Finally x=5

Remember that x is the number of math problems Mila solved, so this means that Mila solved 5 math problems in 55 minutes.