Question

Determine whether AABC has no solution or one solution. Then solve the triangle if possible.

A = 120, a=7, b= 4

A.) one solution; c=4.1: B-29.7°C -30.3°

B.) one solution; c = 4.1: B = 30.30; C = 29.7°

C.) one solution; c= 7; B = 29.7º; C = 120°

D.) no solution

Answer 1

A.) one solution; c ≈ 4,1; B ≈ 29,7°; C = 30,3°

Explanation:

We will be using the Law of Sines:

Solving for Angle Measures

`(sin∠C)/(c) = (sin∠B)/(b) = (sin∠A)/(a)`

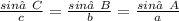
In the end, use the
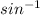`sin^(-1)` function or else you will throw off your answer.

Solving for Sides

`(c)/(sin∠C) = (b)/(sin∠B) = (a)/(sin∠A)`

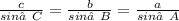
Given instructions:

120° = A

7 = a

4 = b

Now, we have to solve for m∠B, since its side has already been defined, also, it is because angle A and side a have all information filled in:

`(sin\: ∠B)/(4) = (sin\: 120°)/(7) \\ \\ (4sin\: 120°)/(7) = sin\: ∠B \\ \\ (2√(3))/(7) = sin\: ∠B \\ \\ *\: sin^(-1) (2√(3))/(7) ≈ 29,66128776° \\ \\ 29,7° ≈ m∠B`

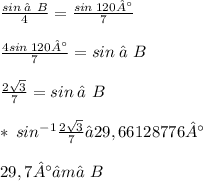
Now that we have the measure of the second angle, we can use the Triangular Interior Angles Theorem to find the third angle measure:

`29,7° + 120° + C = 180°`

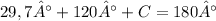
149,7° +
`C` = 180°

-149,7° - 149,7°

_____________________________

`30,3° = C`

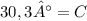
Now, we have to find side c. We could use the information for angle B and side b:

`(c)/(30,3) = (4)/(29,7) \\ \\ (4 * 30,3)/(29,7) = (121,2)/(29,7) = 4(8)/(99)\\ \\ 4,1 ≈ c`

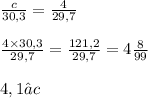
Now, everything has been defined!

I am delighted to assist you anytime.