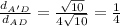Question

Suppose you have AB on a coordinate plane located at A(-3,-4) and B(5,-4)

Under a dilation centered at (9,0), AB becomes A'B' with coordinates A' (6,-1)

and B'(8,-1). What is the scale factor for this dilation?

What’s the answer

Answer 1

The scale factor is 1/4

Explanation:

There are two ways to get this answer:

1. Graphically: After representing the point in the graph, you can count the distance between each point on the x and y axis, and the dilation point D).

The distance in the y-axis between A'B' and D is 1, while AB and D is 4.

The distance in the x-axis between A and D is 12, while A' and D is 3.

We can see that in both axis the distance is reduced by 1/4.
`(y_(axis) =(1)/(4)); (x_(axis) =(3)/(12)=(1)/(4))`

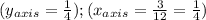
2. Mathematically: To do this is necessary to find the distance between for example point A and A' with D, and then find the proportion
`(A')/(A)`

`d_(AD)=\sqrt{(X_(D)-X_(A))^(2) +(Y_(D)-Y_(A))^(2) }`

`d_(AD)=\sqrt{(9-(-3))^(2) +(0-(-4))^(2) } =\sqrt{(12)^(2) +(4)^(2) }`

`d_(AD)=\sqrt160} =4√(10)`

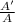
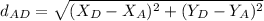
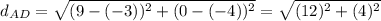
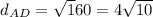
Following the same procedure:

`d_(A'D)=\sqrt{(9-6)^(2) +(0-(-1))^(2) }=\sqrt{(3)^(2) +(1)^(2) }=√(10)`

Therefore, the proportion is
`(d_(A'D))/(d_(AD))=(√(10))/(4√(10)) =(1)/(4)`