Question

HELPPPPP!!!! ASAP

A projectile is thrown upward so that its distance above the ground after t seconds is given by the function h(t) = -16t2 + 640t. After how many seconds does the projectile take to reach its maximum height? Show your work for full credit.

Answer 1

Answer: The projectile reaches its maximum height after 20 seconds.

Explanation:

Given the function:

`h(t) = -16t^2 + 640t`

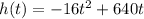
You can following formula (which gives the x -coordinate of the vertex of the parabola) in order to find after how many seconds the projectile takes to reach its maximum height:

`x=t=-(b)/(2a)`

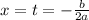
In this case you can identify that the values of "a" and "b" are:

`a=-16\\b=640`

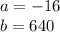
Then, substituting values into the formula, you get the following result:

`t=-(640)/(2(-16))\\\\t=20`

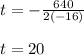
Therefore,based on this, the conclusion is: The projectile reaches its maximum height after 20 seconds.