Question

Assume the upper arm length of males over 20 years old in the United States is approximately Normal with mean 39.3 centimeters (cm) and standard deviation 2.4 cm. Use the 68–95–99.7 rule to answer the given questions. (a) What range of lengths covers almost all, 99.7%, of this distribution? Enter your answers rounded to one decimal place.

Answer 1

The lengths from 32.1cm to 46.5cm covers 99.7% of this distribution.

Explanation:

The 68-95-99.7 rule states that, for normally distributed measures:

68% of the values are within 1 standard deviation of the mean.

95% of the values are within 2 standard deviations of the mean.

99.7% of the values are within 3 standard deviations of the mean.

(a) What range of lengths covers almost all, 99.7%, of this distribution?

Those are those values within 3 standard deviations of the mean. So

From A to B, in which

`A = \mu - 3\sigma = 39.3 - 3(2.4) = 32.1`

`A = \mu + 3\sigma = 39.3 + 3(2.4) = 46.5`

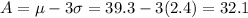
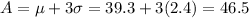
The lengths from 32.1cm to 46.5cm covers 99.7% of this distribution.

Answer 2

The solution is:

The range of lengths covering 99.7 % in cm is: ( 32.1 ; 46.5 )

For Normal Distribution, The Empirical Rule ( μ ; σ ) establishes:

• 68 % approximately of all vales will be in the interval ( μ ± σ )

• 95 % approximately of all vales will be in the interval ( μ ± 2σ )

• 99.7 % approximately of all vales will be in the interval ( μ ± 3σ )

a) According to that 99.7 % of all values will be in the interval:

(39.3 ± 3×2.4)

That is: ( 39.3 - 7.2 ; 39.3 + 7.2)

or ( 32.1 ; 46.5 )