Answer:
A. 0.72
Explanation:
The football is going to hit the ground when
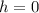 .
.
So we have to solve the following second order polynomial.

We do this by the bhaskara formula.
Explanation of the bhaskara formula:
Given a second order polynomial expressed by the following equation:
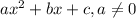 .
.
This polynomial has roots
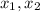 such that
such that
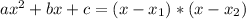 , given by the following formulas:
, given by the following formulas:
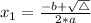
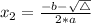
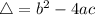
For the polynomial
 , we have that:
, we have that:
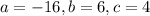 .
.
So
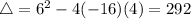
The solution is the positive root(there is no negative time).
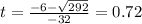
The correct answer is:
A. 0.72