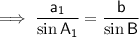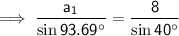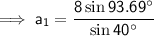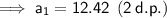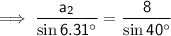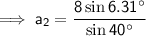Question

Please solve the law of sines ambiguous case question. Please explain the questiom concisely and succinctly since I get confused easily with too complicated steps.​

Answer 1

Two triangles are produced.

C₁ ≈ 46.31° (2 d.p.)

A₁ ≈ 93.69° (2 d.p.)

a₁ ≈ 12.42 (2 d.p.)

C₂ ≈ 133.69° (2 d.p.)

A₂ ≈ 6.31° (2 d.p.)

a₂ ≈ 1.37 (2 d.p.)

Explanation:

Given:

• b = 8
• c = 9
• B = 40°

Two triangles can be produced with the given information (see attached).

Angle C can be acute (less than 90°) and obtuse (greater than 90° and less than 180°).

Use the Sine Rule to find the measure of angle C.

Sine Rule

`\sf (\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

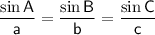
(where A, B and C are the angles and a, b and c are the sides opposite the angles).

Substitute the given information into the Sine Rule formula and solve for C:

`\implies \sf (\sin 40^(\circ))/(8)=(\sin C)/(9)`

`\implies \sf \sin C= (9\sin 40^(\circ))/(8)`

`\implies \sf C= \sin^(-1)\left((9\sin 40^(\circ))/(8)\right)`

`\implies \sf C=46.31^(\circ)\:\: (2\:d.p.)`

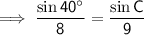
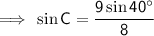
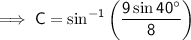
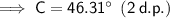
The found angle is acute and is therefore the measure of angle C₁.

If C₁ is acute, then its supplement is obtuse as sin θ = sin (180° - θ), where 90° < θ < 180°.

Therefore, angle C₂ is:

`\implies \sf 180^(\circ)-46.31^(\circ)=133.69^(\circ)\:(2\:d.p.)`

Therefore:

• C₁ ≈ 46.31° (2 d.p.)
• C₂ ≈ 133.69° (2 d.p.)

Now we have found angles C₁ and C₂, use the theorem of interior angles of a triangle sum to 180° to find A₁ and A₂.

`\implies \sf A_1+B_1+C_1=180^(\circ)`

`\implies \sf A_1+40^(\circ)+46.31^(\circ)=180^(\circ)`

`\implies \sf A_1=93.69^(\circ)`

`\implies \sf A_2+B_2+C_2=180^(\circ)`

`\implies \sf A_2+40^(\circ)+133.69^(\circ)=180^(\circ)`

`\implies \sf A_2=6.31^(\circ)`

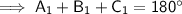
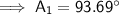
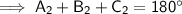
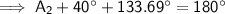
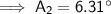
Finally, use the Sine Rule again to find the measure of side a for each triangle.

`\sf (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

`\implies \sf (a_1)/(\sin A_1)=(b)/(\sin B)`

`\implies \sf (a_1)/(\sin 93.69^(\circ))=(8)/(\sin 40^(\circ))`

`\implies \sf a_1=(8\sin 93.69^(\circ))/(\sin 40^(\circ))`

`\implies \sf a_1=12.42\:\:(2 \:d.p.)`

`\implies \sf (a_2)/(\sin A_2)=(b)/(\sin B)`

`\implies \sf (a_2)/(\sin 6.31^(\circ))=(8)/(\sin 40^(\circ))`

`\implies \sf a_2=(8 \sin 6.31^(\circ))/(\sin 40^(\circ))`

`\implies \sf a_2=1.37\:\:(2\:d.p.)`