Question

Determine if a metal rod of 2.8m can fit into a rectangular crate with dimensions 0.8m, 1.2m and 2.3m

the answer is no and the length of the rod would be 2.71m long but how do you get this?????

Answer 1

The metal rod cannot fit into the rectangular crate

The maximum length that can fit is 2.71 m

Explanation:

step 1

Find the diagonal of the base of the rectangular crate

Applying the Pythagoras Theorem

Let

d ----> the diagonal of the base

`d^2=0.8^2+1.2^2`

`d^2=2.08`

`d=1.44\ m`

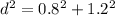
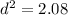
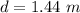
step 2

Find the diagonal of the crate

Let

D ----> the diagonal of the crate

`D^2=d^2+h^2`

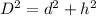
where

d is the diagonal of the base

h is the height of the crate

we have

`d=1.44\ m`

`h=2.3\ m`

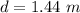
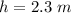
substitute the values

`D^2=1.44^2+2.3^2`

`D^2=7.36`

`D=2.71\ m`

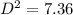
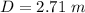
therefore

The metal rod cannot fit into the rectangular crate

The maximum length that can fit is 2.71 m