Question

Working​ together, Rick and Juanita can complete a job in 6 hr. It would take Rick 9 hr longer than Juanita to do the job alone. How long would it take Juanita​ alone? Round your answer to the nearest​ tenth, if necessary.

Answer 1

Explanation

this is the equation r+j=6

this is too r+9=j

from the equation you can tell that r=j-9 if u re=arrange it

now you put r=j-9 into one of the equation up there ↑

j-9+j=6

2j=15

j=7.5

Answer 2

Juanita Alone will take 9 hours to complete the job.

Solution:

For sake of simplicity let’s assume complete job be represented by W.

Job done by Juanita and Rick together in 6 hours is complete job = W

So job done by Juanita and Rick together in 1 hour =
`(W)/(6)`

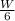
Lets assume number of hours needed by Juanita to complete W work = x hrs

And since Rick takes 9 hours more than Juanita , so number of hours needed by Juanita to complete W work = (x + 9) hrs

Work done by Juanita in 1 hour =
`(W)/(x)`

Work done by Rick in 1 hour =
`(W)/((x + 9))`

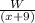
So when they work together, work done in 1 hour =
`(W)/(x) + (W)/((x + 9))`

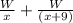
Also initially we evaluated that work done by them in 1 hr =
`(W)/(6)`

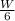
So
`(W)/(x) + (W)/((x + 9))` =
`(W)/(6)`

`\mathrm{W}\left((1)/(x)+(1)/(x+9)\right)=(W)/(6)` =
`(W)/(6)`

`(1)/(x)+(1)/(x+9)=(1)/(6)`

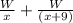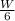
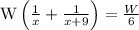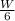
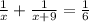
On cross-multiplication we get

`((x+9)+x)/(x(x+9))=(1)/(6)`

`(2 x+9)/(x^(2)+9 x)=(1)/(6)`

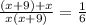
Again on cross-multiplication we get,

`\begin{array}{c}{12 x+54=x^(2)+9 x} \\ {x^(2)-3 x-54=0}\end{array}`

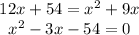
On splitting the middle term we get

`=x^(2)-9 x+6 x-54=0`

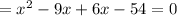
x( x – 9) +6( x – 9 ) = 0

(x+6) (x-9) = 0

When x + 6 = 0, x = -6

When x – 9 = 0, x = 9

Since x is number of hours, it cannot be negative in given case. So required solution is x = 9.

Hence Juanita Alone will take 9 hours to complete the job.