Question

The product of the slopes of perpendicular lines equals what?

Answer 1

If two non-vertical lines are perpendicular, then their slopes are opposite reciprocals giving you -1.

:) Hope this helps.

Answer 2

The product of the slopes of perpendicular lines equals -1

Solution:

Need to determine product of slope of perpendicular lines.

Product of slopes of perpendicular lines is always equal to -1.

lets verify this.

let consider following two equation of perpendicular lines

2x – y = 1

x + 2y = 2

Now evaluate slope of each line by representing them in slop intercept form that is y = mx + c

Where coefficient of x represents slope m.

Representing first line in slope intercept form we get

y = 2x – 1

On comparing above equation with slope intercept form we can say that its slope is 2.

Similarly representing x + 2y = 2 equation in slope intercept form we get

`y=-(1)/(2) x+1`

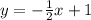
On comparing above equation with slope intercept form we can say that its slope is
`(-1)/(2)`

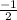
On multiplying slopes of two perpendicular lines we get,

`2 *\left(-(1)/(2)\right)=-1`

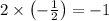
Hence product of slope of perpendicular line is -1