Question

Pls help!!!!1! domain problem

Answer 1

x ∈ R, x ≠ 1

Explanation:

f(g(x))

= f(
`(4)/(x-2)` )

=
`(1)/((4)/(x-2)+4 )`

=
`(1)/((4+4(x-2))/(x-2) )`

=
`(1)/((4+4x-8)/(x-2) )`

=
`(x-2)/(4x-4)`

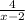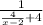
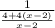
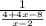
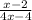
The denominator of f(g(x)) cannot be zero as this would make f(g(x)) undefined. Equating the denominator to zero and solving gives the value that x cannot be, that is

4x - 4 = 0 ⇒ 4x = 4 ⇒ x = 1 ← excluded value

Domain : x ∈ R, x ≠ 1, that is

(- ∞, 1) ∪ (1, ∞ ) ← in interval notation