Answer:
110 meters is the distance where they will intersect
Step-by-step explanation:
given,
liquid density = 1900 kg/m³
distance of upper hole = 19 m
distance of lower hole = 117 m
acceleration due to gravity = 9.8 m/s²
the speed at each point
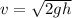
for upper hole

v = 19.29 m/s
lower hole
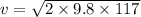
v = 47.88 m/s
The path for each is parabolic
x = v t


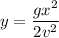
we get
upper hole
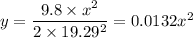 lower hole
lower hole
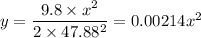 y for upper hole = 80 + y for lower hole
y for upper hole = 80 + y for lower hole
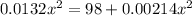
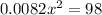
x = 109.32 meters
110 meters is the distance where they will intersect