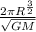Question

The motivation for Isaac Newton to discover his laws of motion was to explain the properties of planetary orbits that were observed by Tycho Brahe and analyzed by Johannes Kepler. A good starting point for understanding this (as well as the speed of the space shuttle and the height of geostationary satellites) is the simplest orbit - a circular one. This problem concerns the properties of circular orbits for a satellite orbiting a planet of mass M. Use G for the universal gravitational constant. Find the orbital period T.

Answer 1

Step-by-step explanation:

We know that , for an object to remain in circular motion , a force towards centre is required which is called centripetal force. In the circular motion of

satellites around planet , this force is provided by the gravitational attraction between satellite and planet.

If M be the mass of planet and m be the mass of satellite, G be gravitational constant and R be the distance between planet and satellite or R be the radius of orbit

Gravitational force = G Mm / R²

If v be the velocity with which satellite is orbiting

centripetal force

= m v² /R

Centripetal force = gravitational attraction

m v² /R = G Mm / R²

v =
`\sqrt{(GM)/(R) }`

Time period = time the satellite takes to make one rotation

= distance / orbital velocity

= 2πR/ v

=
`(2\pi R√(R) )/(√(GM) )`

T =
`(2\pi R^(3)/(2) )/(√(GM) )`