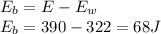Answer:
a) 390J
b) 322J
c) 68J
Step-by-step explanation:
We need to calculate the power given by the battery. the power is given by:
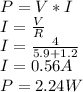
Watts is J/s so:
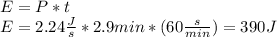
The thermal energy in the wire is given by:

And the the dissipated thermal energy in the battery will be the remainig energy: