Question

Titan has a radius of 2600.0 km and a mean density of 2.1 g/cm3. Earth's Moon has a radius of 1737.0 km and a mean density of 3.4 g/cm3. What is the ratio of gravitational acceleration on Titan compared to that on the Moon? The gravitational constant is G = 6.67 × 10-11 m3 kg-1 s-2.

Answer 1

`(g_1)/(g_2)=0.92`

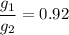
Step-by-step explanation:

It is given that,

The radius of Titan,
`r_1=2600\ km=26* 10^5\ m`

Density of Titan,
`d_1=2.1\ g/cm^3=2100\ kg/m^3`

Radius of moon,
`r_2=1737\ km=1737* 10^3\ m`

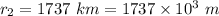
Density of the moon,
`d_2=3.4\ g/cm^3=3400\ kg/m^3`

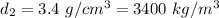
Value of gravitational constant,
`G=6.67* 10^(-11)\ m^3kg^(-1)s^(-2)`

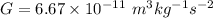
The gravitational acceleration is given by :

`g=(GM)/(r^2)`

`g=(G* d* \pi r^2)/(r^2)`

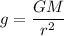
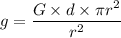
Let g₁ and g₂ are the gravitational acceleration on Titan and on the moon respectively. So,

`(g_1)/(g_2)=((G* d_1* (4/3)\pi r_1^3)/(r_1^2))/((G* d_2* (4/3)\pi r_2^3)/(r_2^2))`

`(g_1)/(g_2)=(d_1r_1)/(d_2r_2)`

`(g_1)/(g_2)=(2100* 26* 10^5)/(3400* 1737* 10^3)`

`(g_1)/(g_2)=0.92`

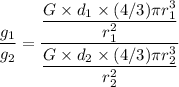
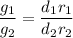
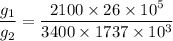
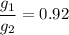
So, the ratio of gravitational acceleration on Titan compared to that on the Moon is 0.92 : 1. Hence, this is the required solution.