Question

Please answerrrr Graph g(x), where f(x) = 4x − 2 and g(x) = f(x + 1). a line labeled g of x that passes through points 0, negative 2 and 1, 2 a line labeled g of x that passes through points 0, negative 3 and 1, 1 a line labeled g of x that passes through points negative 1, negative 2 and 0, 2 a line labeled g of x that passes through points 0, negative 1 and 1, 3

Answer 1

Option 3

Explanation:

Answer 2

a line labeled g of x that passes through points negative 1, negative 2 and 0, 2

Explanation:

we have

`f(x)=4x-2`

`g(x)=f(x+1)`

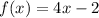
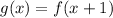
To determine g(x), substitute the variable x by (x+1) in the function f(x)

so

`f(x+1)=4(x+1)-2`

`f(x+1)=4x+4-2`

`f(x+1)=4x+2`

`g(x)=f(x+1)`

`g(x)=4x+2`

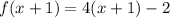
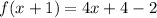
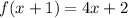
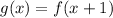
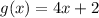
therefore

a line labeled g of x that passes through points negative 1, negative 2 and 0, 2