Question

Prove (x^2)+1/(x^2 )≥x + (1/x )≥2 for x>0​

Answer 1

First of all, let's prove that

`x+(1)/(x)\geq 2,\quad x>0`

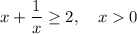
We can rewrite the fraction as

`(x^2+1)/(x)`

And the inequality as

`(x^2+1)/(x)-2\geq 0`

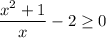
Again, we can rewrite as

`(x^2-2x+1)/(x)\geq 0 \iff ((x-1)^2)/(x)\geq 0`

The numerator is a square, so it is always greater than or equal to zero.

The denominator is positive, because we're assuming x>0.

So, this is a fraction between positive numbers, and it is always positive, and the first part is finished.

As for the second part, we have

`x^2+(1)/(x^2) \geq x+(1)/(x) \iff x^2+(1)/(x^2)-x-(1)/(x) \geq 0 \iff ((x - 1)^2 (x^2 + x + 1))/(x^2) \geq 0`

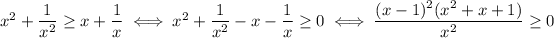
The numerator is not the product of a square (always greater than or equal to zero) and a quadratic equation with no solutions and positive leading coefficient (always positive), so it's always greater than or equal to zero. The denominator is x^2, and since x>0 by hypothesis, it is positive. This ends the proof.