Step-by-step explanation:
The given data is as follows.
Temperature =
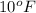
Density (
 ) = 62.4
) = 62.4
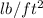
Pressure drop = 3.55
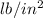
= 511.6
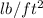 (as 1
(as 1
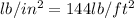 )
)
Height of manometer = 48 inch = 4 ft (as 1 inch = 0.0833)
g = 9.81
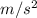
= 32.18
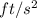 (as 1
(as 1
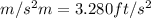 )
)
(a) Specific gravity of monometric fluid
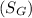 will be calculated as follows.
will be calculated as follows.
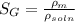
where,
 = density of manometric fluid
= density of manometric fluid
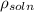 = density of standard fluid (water) = 1000 g/ml
= density of standard fluid (water) = 1000 g/ml
So,
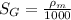

where,
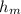 = height of manometric fluid
= height of manometric fluid
 = density of manometric fluid
= density of manometric fluid
Now, putting the given values into the above formula as follows.

511.6
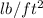 =
=
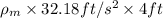
 = 3.97
= 3.97
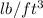
Therefore, calculate the value of
 as follows.
as follows.
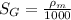
=
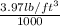
=
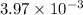
And, for mercury
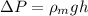
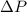 =
=

= 109283.28
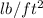
= 39246.99 mm Hg (1
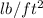 = 0.3591 mm Hg)
= 0.3591 mm Hg)
Thus, we can conclude that the pressure drop in millimeters of mercury is 39246.99 mm Hg.